http://www.songho.ca/opengl/gl_vbo.html
OpenGL Vertex Buffer Object (VBO)
Related Topics: Vertex Array, Display List, Pixel Buffer Object
Download: vbo.zip, vboSimple.zip
GL_ARB_vertex_buffer_object extension is intended to enhance the performance of OpenGL by providing the benefits of vertex array and display list, while avoiding downsides of their implementations. Vertex buffer object (VBO) allows vertex array data to be stored in high-performance graphics memory on the server side and promotes efficient data transfer. If the buffer object is used to store pixel data, it is called Pixel Buffer Object (PBO).
Using vertex array can reduce the number of function calls and redundant usage of the shared vertices. However, the disadvantage of vertex array is that vertex array functions are in the client state and the data in the arrays must be re-sent to the server each time when it is referenced.
On the other hand, display list is server side function, so it does not suffer from overhead of data transfer. But, once a display list is compiled, the data in the display list cannot be modified.
Vertex buffer object (VBO) creates "buffer objects" for vertex attributes in high-performance memory on the server side and provides same access functions to reference the arrays, which are used in vertex arrays, such as glVertexPointer(), glNormalPointer(), glTexCoordPointer(), etc.
The memory manager in vertex buffer object will put the buffer objects into the best place of memory based on user's hints: "target" and "usage" mode. Therefore, the memory manager can optimize the buffers by balancing between 3 kinds of memory: system, AGP and video memory.
Unlike display lists, the data in vertex buffer object can be read and updated by mapping the buffer into client's memory space.
Another important advantage of VBO is sharing the buffer objects with many clients, like display lists and textures. Since VBO is on the server's side, multiple clients will be able to access the same buffer with the corresponding identifier.
Creating VBO
Creating a VBO requires 3 steps;
- Generate a new buffer object with glGenBuffersARB().
- Bind the buffer object with glBindBufferARB().
- Copy vertex data to the buffer object with glBufferDataARB().
glGenBuffersARB()
glGenBuffersARB() creates buffer objects and returns the identifiers of the buffer objects. It requires 2 parameters: the first one is the number of buffer objects to create, and the second parameter is the address of a GLuint variable or array to store a single ID or multiple IDs.
glBindBufferARB()
Once the buffer object has been created, we need to hook the buffer object with the corresponding ID before using the buffer object. glBindBufferARB() takes 2 parameters: target and ID.
Target is a hint to tell VBO whether this buffer object will store vertex array data or index array data: GL_ARRAY_BUFFER_ARB, or GL_ELEMENT_ARRAY_BUFFER_ARB. Any vertex attributes, such as vertex coordinates, texture coordinates, normals and color component arrays should use GL_ARRAY_BUFFER_ARB. Index array which is used for glDraw[Range]Elements() should be tied with GL_ELEMENT_ARRAY_BUFFER_ARB. Note that this target flag assists VBO to decide the most efficient locations of buffer objects, for example, some systems may prefer indices in AGP or system memory, and vertices in video memory.
Once glBindBufferARB() is first called, VBO initializes the buffer with a zero-sized memory buffer and set the initial VBO states, such as usage and access properties.
glBufferDataARB()
You can copy the data into the buffer object with glBufferDataARB() when the buffer has been initialized.
Again, the first parameter, target would be GL_ARRAY_BUFFER_ARB or GL_ELEMENT_ARRAY_BUFFER_ARB. Size is the number of bytes of data to transfer. The third parameter is the pointer to the array of source data. If data is NULL pointer, then VBO reserves only memory space with the given data size. The last parameter, "usage" flag is another performance hint for VBO to provide how the buffer object is going to be used: static, dynamic or stream, and read, copy or draw.
VBO specifies 9 enumerated values for usage flags;
GL_STATIC_DRAW_ARB GL_STATIC_READ_ARB GL_STATIC_COPY_ARB GL_DYNAMIC_DRAW_ARB GL_DYNAMIC_READ_ARB GL_DYNAMIC_COPY_ARB GL_STREAM_DRAW_ARB GL_STREAM_READ_ARB GL_STREAM_COPY_ARB
"Static" means the data in VBO will not be changed (specified once and used many times), "dynamic" means the data will be changed frequently (specified and used repeatedly), and "stream" means the data will be changed every frame (specified once and used once). "Draw" means the data will be sent to GPU in order to draw (application to GL), "read" means the data will be read by the client's application (GL to application), and "copy" means the data will be used both drawing and reading (GL to GL).
Note that only draw token is useful for VBO, and copy and read token will be become meaningful only for pixel/frame buffer object (PBO or FBO).
VBO memory manager will choose the best memory places for the buffer object based on these usage flags, for example, GL_STATIC_DRAW_ARB and GL_STREAM_DRAW_ARB may use video memory, and GL_DYNAMIC_DRAW_ARB may use AGP memory. Any _READ_ related buffers would be fine in system or AGP memory because the data should be easy to access.
glBufferSubDataARB()
Like glBufferDataARB(), glBufferSubDataARB() is used to copy data into VBO, but it only replaces a range of data into the existing buffer, starting from the given offset. (The total size of the buffer must be set by glBufferDataARB() before using glBufferSubDataARB().)
glDeleteBuffersARB()
You can delete a single VBO or multiple VBOs with glDeleteBuffersARB() if they are not used anymore. After a buffer object is deleted, its contents will be lost.
The following code is an example of creating a single VBO for vertex coordinates. Notice that you can delete the memory allocation for vertex array in your application after you copy data into VBO.
GLuint vboId; // ID of VBO GLfloat* vertices = new GLfloat[vCount*3]; // create vertex array ... // generate a new VBO and get the associated ID glGenBuffersARB(1, &vboId); // bind VBO in order to use glBindBufferARB(GL_ARRAY_BUFFER_ARB, vboId); // upload data to VBO glBufferDataARB(GL_ARRAY_BUFFER_ARB, dataSize, vertices, GL_STATIC_DRAW_ARB); // it is safe to delete after copying data to VBO delete [] vertices; ... // delete VBO when program terminated glDeleteBuffersARB(1, &vboId);
Drawing VBO
Because VBO sits on top of the existing vertex array implementation, rendering VBO is almost same as using vertex array. Only difference is that the pointer to the vertex array is now as an offset into a currently bound buffer object. Therefore, no additional APIs are required to draw a VBO except glBindBufferARB().
// bind VBOs for vertex array and index array glBindBufferARB(GL_ARRAY_BUFFER_ARB, vboId1); // for vertex coordinates glBindBufferARB(GL_ELEMENT_ARRAY_BUFFER_ARB, vboId2); // for indices // do same as vertex array except pointer glEnableClientState(GL_VERTEX_ARRAY); // activate vertex coords array glVertexPointer(3, GL_FLOAT, 0, 0); // last param is offset, not ptr // draw 6 quads using offset of index array glDrawElements(GL_QUADS, 24, GL_UNSIGNED_BYTE, 0); glDisableClientState(GL_VERTEX_ARRAY); // deactivate vertex array // bind with 0, so, switch back to normal pointer operation glBindBufferARB(GL_ARRAY_BUFFER_ARB, 0); glBindBufferARB(GL_ELEMENT_ARRAY_BUFFER_ARB, 0);
Binding the buffer object with 0 switchs off VBO operation. It is a good idea to turn VBO off after use, so normal vertex array operations with absolute pointers will be re-activated.
Updating VBO
The advantage of VBO over display list is the client can read and modify the buffer object data, but display list cannot. The simplest method of updating VBO is copying again new data into the bound VBO with glBufferDataARB() or glBufferSubDataARB(). For this case, your application should have a valid vertex array all the time in your application. That means that you must always have 2 copies of vertex data: one in your application and the other in VBO.
The other way to modify buffer object is to map the buffer object into client's memory, and the client can update data with the pointer to the mapped buffer. The following describes how to map VBO into client's memory and how to access the mapped data.
glMapBufferARB()
VBO provides glMapBufferARB() in order to map the buffer object into client's memory.
If OpenGL is able to map the buffer object into client's address space, glMapBufferARB() returns the pointer to the buffer. Otherwise it returns NULL.
The first parameter, target is mentioned earlier at glBindBufferARB() and the second parameter, access flag specifies what to do with the mapped data: read, write or both.
GL_READ_ONLY_ARB GL_WRITE_ONLY_ARB GL_READ_WRITE_ARB
Note that glMapBufferARB() causes a synchronizing issue. If GPU is still working with the buffer object, glMapBufferARB() will not return until GPU finishes its job with the corresponding buffer object.
To avoid waiting (idle), you can call first glBufferDataARB() with NULL pointer, then call glMapBufferARB(). In this case, the previous data will be discarded and glMapBufferARB() returns a new allocated pointer immediately even if GPU is still working with the previous data.
However, this method is valid only if you want to update entire data set because you discard the previous data. If you want to change only portion of data or to read data, you better not release the previous data.
glUnmapBufferARB()
After modifying the data of VBO, it must be unmapped the buffer object from the client's memory. glUnmapBufferARB() returns GL_TRUE if success. When it returns GL_FALSE, the contents of VBO become corrupted while the buffer was mapped. The corruption results from screen resolution change or window system specific events. In this case, the data must be resubmitted.
Here is a sample code to modify VBO with mapping method.
// bind then map the VBO glBindBufferARB(GL_ARRAY_BUFFER_ARB, vboId); float* ptr = (float*)glMapBufferARB(GL_ARRAY_BUFFER_ARB, GL_WRITE_ONLY_ARB); // if the pointer is valid(mapped), update VBO if(ptr) { updateMyVBO(ptr, ...); // modify buffer data glUnmapBufferARB(GL_ARRAY_BUFFER_ARB); // unmap it after use } // you can draw the updated VBO ...
Example
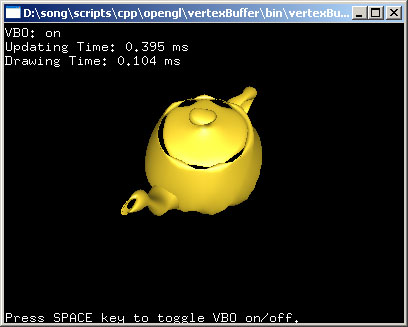
This demo application makes a VBO wobbling in and out along normals. It maps a VBO and updates its vertices every frame with the pointer to the mapped buffer. You can compare the performace with a traditional vertex array implementation.
It uses 2 vertex buffers; one for both vertex coords and normals, and the other stores index array only.
Download the source and binary: vbo.zip, vboSimple.zip.
vboSimple is a very simple example to draw a cube using VBO and Vertex Array. You can easily see what is common and what is different between VBO and VA.
I also include a makefile (Makefile.linux) for linux system in src folder, so you can build an executable on your linux box, for example:
.jpg)














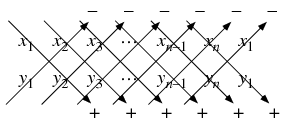
 , at time
, at time 















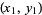 , ...,
, ..., 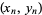 is
is 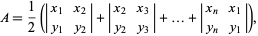
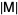 denotes a
denotes a